Rayleigh scattering occurs at particles that are small relative to the wavelength of incoming radiation. In practice Rayleigh scattering involves the scattering of visible light by molecules or particles having a radius of up to about a tenth of the wavelength of the light.
Rayleigh scattering can be explained in terms of an ensemble of dipole emitters, in which the particles themselves radiate as dipoles. A more accurate treatment is based on density fluctuations in the scattering medium.
Wavelength dependency
Rayleigh scattering does not affect the wavelength of the incident light: the wavelength of the incoming and outgoing radiation remains the same.
The amount of Rayleigh scattering that takes place varies inversely with the fourth power of the wavelength:
σsRayleigh(λ) = ~ λ-4
In the Earth's atmosphere, therefore, ultraviolet radiation is usually scattered before reaching the surface.
Distribution of scattered light
The phase function P(φ) gives the distribution of scattered intensity as a function of scattering angle. If the incoming light is unpolarized the intensity of the scattered radiation is proportional to the scattering angle, Θ:
I ~ (1 + cos2Θ)
The angular distribution of Rayleigh scattering is symmetrical in the plane normal to the incident direction of the light, and so the forward scatter equals the backwards scatter.
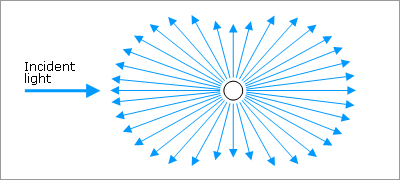
Fig 2.2.2.2.1.1: Rayleigh phase function
Image: AT2-ELS
Scattering coefficient
For a group of scattering particles, the Rayleigh scattering is given by the Rayleigh scattering coefficient that is the product of the number of particles (N) per unit volume the times the scattering cross-section of the individual particle.
From a macroscopic point of view, the complex interactions of radiation with the atoms or molecules in a medium are given by a single parameter, the complex index of refraction of the medium:
N = nr + nii
where the real part nr controls the effective phase speed of electromagnetic waves propagating through the medium and the imaginary part ni describes the rate of absorption of the wave.