Mie scattering occurs at 'large' particles, such as those found in aerosols, droplets and suspended matter in liquids. It is produced by particles having a diameter approximately equal to or larger than the wavelength of the incoming radiation. Strictly speaking, Mie theory only applies to spherical particles. Mie theory allows us to calculate scattering phase function, scattering cross-sections and absorption cross-sections using the refractive index and the Mie size parameter. However Mie scattering in general is not so strongly determined.
Mie scattering can be explained in terms of a coherent scattering from many individual particles. For spherical particles, Mie scattering can be computed from the refractive index using the Maxwell equations. However, most large particles present in the atmosphere are not spherical.
Wavelength dependency
As is also the case with Rayleigh scattering, Mie scattering does not affect the wavelength of the incident light: the wavelength of the incoming and outgoing radiation remains the same.
Unlike Rayleigh scattering, however, Mie scattering is not strongly dependent on the wavelength of the incoming radiation. As a result of this factor, Mie scattering has a 'whitening' effect.
The amount of Mie scattering that takes place at a wavelength λ is
σsMie(λ) = ~ λ0...λ-4
Distribution of scattered light
Depending on the Mie parameter, α (the ratio of the particle size to the wavelength), forward scattering is strongly favoured.
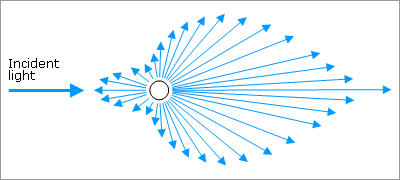
Fig 2.2.2.2.2.1: Mie phase function
Image: AT2-ELS
The larger the particles, the stronger the forward peak.
The angular distribution of Mie scattering is a complex function of particle size even for spherical particles.
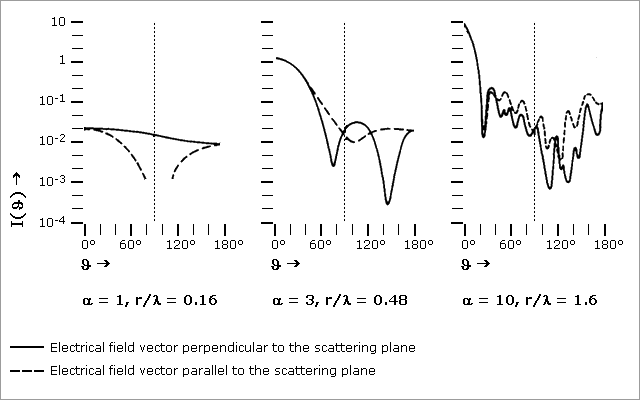
Fig 2.2.2.2.2.2: Mie phase function for particle size.
Normalised differential scattering cross-section as a function of the
scattering angle, Φ, for spherical dielectric
aerosol particles with refractive index n = 1.5 and for three
different particle size parameters, α = 2·π·r/λ.
Image: AT2-ELS
Extinction by Mie scattering
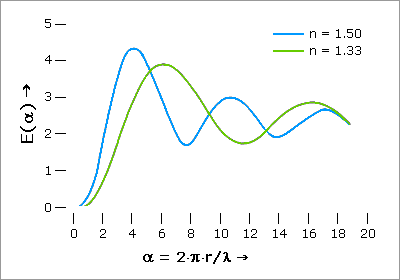
Fig 2.2.2.2.2.3: Mie extinction function.
Extinction functions, E, normalised for particle cross-section, as a function
of the particle size parameter, α = 2·π·r/λ for
two materials of different refractive indices, n. (Hodkinson, 1966).
At very large values of α E(α) converges to 2. For an explanation
see, e.g. Van de Hulst (1981).
Image: AT2-ELS
In general scattering on large particles can not be treated quantitatively because
- most particles are not spherical;
- the composition of particles (and thus the refractive index, n) is not well known;
- the size distribution of particles is not well known;
- changes in humidity can have a large impact on the optical properties of particles;
- absorption in aerosols can often not be neglected.
Polarisation of scattered light
In general, Mie scattering is not polarising.