Inhaltsverzeichnis

Der Forschungsbereich der neuronalen Netze, auch konnektionistische Systeme genannt, obwohl schon vor 30 Jahren bekannt, gewann erst im Laufe der letzten Jahre immer mehr an Bedeutung und wird heute als ein wichtiges Gebiet der Informatik betrachtet. Hier werden in den nächsten Jahren große Fortschritte erwartet. Lange Zeit bestanden Anwendungen neuronaler Netze nur aus der Verwendung innerhalb der Raumfahrtforschung oder Rüstungsindustrie, so z.B. für die Steuerung von .Waffensystemen oder der Auswertung von Luftbildern zur Feindaufklärung. Später kamen zivile Gebiete hinzu, wie Oberflächenanalysen oder Qualitätskontrollen von Werkstoffen bzw. Robotersteuerungen für gefährliche Aufgaben. Seit einigen Jahren wird auch verstärkt versucht medizinische Diagnoseprobleme mit Hilfe von Methoden der modernen künstlichen Intelligenz, kurz KI, zu lösen. Die meisten Bemühungen wurden auf dem Gebiet der Expertensysteme angestellt, wo anhand der Auswertung regelbasierten Expertenwissens, versucht wird Diagnosen zu stellen, diese Methode ließ sich allerdings nur begrenzt auf die Auswertung klarer Symptome anwenden. Die andere bedeutende Strecke der KI ist die Verwendung neuronaler Netze, die aus Neuronen und deren Verbindungen untereinander, ähnlich dem menschlichen Gehirn, bestehend, gelerntes Wissen abbilden und nutzbar machen können. Als Beispiel für eine Anwendung innerhalb der Medizin, sei die Entwicklung von Retinaimplantaten genannt, die, gekoppelt mit neuronalen Netzen, blinden Patienten ermöglichen sollen, wieder zu sehen. In die Reihe medizinischer Anwendungen neuronaler Netze soll sich die vorliegende Arbeit eingliedern.

1. Was versteht man unter neuronalen Netzen
1.1. Grundlegende Ideen

Diese Ausführungen sind als kurze Erläuterung zum Thema "Neuronale Netze" zu betrachten, sie sind keinesfalls vollständig. Nähere, tiefergehende Informationen entnehmen Sie bitte den angegebenen Literaturstellen. Der Traum von "Künstlicher Intelligenz" (KI) ist als Teilaspekt der Informatik stets einer ihrer wesentlichen Triebkräfte gewesen. Noch vor den faszinierenden Ideen von J.v. Neumann, A.Turing und K.Zuse in den 50er Jahren (die Architektur und Programmierung unserer heutigen Computer begründeten) sind die Wurzeln der "Neuroinformatik" zu finden : W.McCulloch und W.Pitts /2 S.28/ beschrieben 1943 ein abstraktes Neuronen-Modell als Baustein einer Schwellwertlogik. Erste hoffnungsvolle Experimente mit "Simulierten Neuronalen Netzen" (SNN) zum Muster-Erkennen und -lernen wurden von F.Rosenblatt, B.Widrow und K.Steinbuch um 1960 vorgestellt. 1969 bewiesen jedoch M.Minsky und S.Papert in ihrem einflußreichen Buch "Perceptrons" deren grundsätzliche Beschränktheit und stoppten somit de facto die Forschung. Um KI zu erreichen, setzte die Mehrheit der Forscher damals auf Symbolverarbeitung/Programmierung (in LISP). Trotz beachtlicher Erfolge (z.B. "Expertensysteme") zeichnete sich aber Mitte der 80er Jahre eine KI-Krise ab. "Harte" Probleme (z.B. Mustererkennung) stießen oft an die Grenzen des Machbaren. Sie erforderten lange Rechenzeiten mit Millionen von Verarbeitungsschritten. Vergleicht man die Arbeitsgeschwindigkeiten moderner Computer (Nanosekunden) mit Nervenzellen (Millisekunden), dann folgt aus unserer Reaktionszeit von etwa 1/2 Sekunde in der wir ein Bild erkennen , daß das biologische System nur etwa 100 Verarbeitungsschritte benötigt. Diese Leistung ist in der massiven Parallelverarbeitung unseres Nervensystems begründet. Wegen absehbarer physikal. Grenzen in der VLSI-Technologie (Lichtgeschwindigkeit , Quanteneffekte bei dünnen Leitern), ist man sich heute darüber einig, daß Leistungssteigerungen in den erforderlichen Größenordnungen, nur durch Parallelverarbeitung zu erreichen sind. Als ein erfolgreicher Lösungsansatz wurde dabei die Simulation der Struktur von Nervenverbänden wiederentdeckt Einige Forscher ließen sich nicht durch das vernichtende Urteil von Minsky und Papert davon abhalten diese Feld weiter zu beackern. Inzwischen stellte sich heraus, daß die Kritik nicht für komplexe Netze gilt. Die z.B. 1986 unter dem Schlagwort "PDP" (Parallel Distributed Processing) von D.Rumelhart und J.McClelland publizierten Forschungsergebnisse /2 S.32/ zu Assoziativspeichern mit Fehlertoleranz, Muster-Erkennung und - Vervollständigung , Selbstorganisation und Lernen durch Training an Beispielen --- alles "harte" Probleme der KI --- beeindruckten weltweit und haben jetzt zu einem "Paradigmenwechsel" geführt. Die Synthese von Symbolverarbeitung (z.B. für sequentielle Problemlösungsstrategien mit heuristischen Regeln in Wissensbasierten Systemen) und "Simulation Neuronaler Netze" (für Sensorik, Mustererkennung und Lernen) verspricht aus der bestehenden KI-Krise herauszuführen .

1.2. Nervenzellen und neurologische Erkenntnisse

Bevor wir von der Simulation der Nervennetze sprechen, sollten wir uns an die Funktionsweise des biologischen Systems erinnern: Das menschliche Gehirn besteht aus mindestens 10 Milliarden Neuronen, den Bausteinen des Nervensystems. Die Nervenzelle kann als eine Prozessoreinheit angesehen werden, die Signale von vielen anderen Neuronen über sogenannte Synapsen an ihren Dendriten erhält (Bild 1).

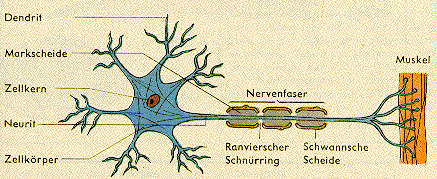
Bild 1: Schema einer Nervenzelle

Man unterscheidet exitatorische (verstärkende) und inhibitorische (schwächende) Synapsen, deren Signale in der Nervenzelle "verrechnet" werden. Liegt das Ergebnis unter einem internen Schwellwert, dann passiert nichts. Nur wenn die Schwelle überschritten wird, dann ("Alles-oder-Nichts"-Regel) "feuert" die Nervenzelle d.h. sie sendet einen elektrischen Impuls von ca. 100mV/1ms über das Axon zu ihren Synapsen, die wiederum mit anderen Neuronen verknüpft sind. Der Informationsfluß wechselt dabei zwischen chemischer und elektrischer Realisation : An den Synapsen bewirkt der elektrische Impuls ein Ausschütten sogenannte Neurotransmitter. Über die synaptischen Spalten gelangen diese an die Rezeptoren in den Dendriten der nachfolgenden Neuronen. Es wird nicht nur ein einziger Impuls, sondern eine Pulsfolge erzeugt, deren Frequenz proportional zur Reizstärke ist. Nach der Hypothese von D.Hebb (1949) findet Lernen durch Modifikation der synaptischen Stärken statt. Eine Verbindung wird verstärkt bei Korrelation von einlaufendem Signal und Aktivität der Zielzelle ("Bahnung"). Von K.Lashley /2 S.28/ wurde 1950 eine wichtige neurobiologische Erkenntnis gewonnen. Er trainierte Ratten ein Labyrinth auf kürzestem Weg zu durchlaufen. Anschließend schädigte er beliebige Hirnareale dieser Tiere, trotzdem fanden sie ihren Weg durchs Labyrinth. Er folgerte daraus, daß die Gedächtnisinformation nicht an bestimmten Orten lokalisiert, sondern verteilt repräsentiert wird. J.Conel zeigte 1970 an histologischen Schnitten der Großhirnrinde von verstorbenen Säuglingen , daß die ersten drei Monate nach der Geburt der entscheidende Zeitraum ist, in dem sich die Verknüpfungen des Nervennetzes selbst organisieren. Tierexperimente bestätigten dabei die Abhängigkeit vom Reizangebot der Umwelt.

1.3. Das abstrakte Neuronenmodell

Nach den damaligen Erkenntnissen entwarfen 1943 W.Mc-Culloch und W.Pitts ein Neuronenmodell, das als Elementarprozessor einer Schwellwertlogik universell einsetzbar ist (Bild 2):

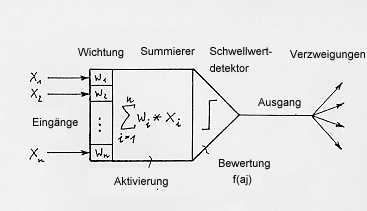
Bild 2:McCulloch u. Pitts (1943) Neuronenmodell

Die Eingangssignale Xi {0,1} werden gemäß der synaptischen Stärke mit (+,-) Wi gewichtet, summiert und mit dem internen Schwellwert verglichen. Nur wenn der Schwellwert überschritten wird, ändert sich der Ausgangswert von 0 auf 1. Es ist leicht zu zeigen (Bild 3), daß damit (je nach Schwellwert und/oder Gewichten) sowohl ODER- als auch UND- (sowie NAND-) Gatter realisiert werden können und somit komplexe logische Verknüpfungen möglich sind.

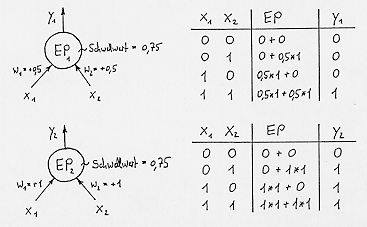
Bild 3: Bsp. für UND- und ODER-Verknüpfungen

1.4. Frühe Experimente mit Simulierten Neuronalen Netzen

Als lernender Klassifikator konnte das "Perceptron" /2 Kap.7.2/ von F.Rosenblatt (1958) Muster erkennen, bestimmte Eigenschaften generalisieren (z.B. horizontal/vertikal) und war robust gegenüber Eingangsrauschen und Störungen. Es bestand aus 3 Schichten : Die "Retina" (zur Erfassung des binären Eingabefeldes) war über feste Gewichte mit der "Assoziationsschicht" verbunden und diese über lernfähige Gewichte mit der Ausgabe (Bild 4). Ziel des Trainings in der Lernphase war es, bei einem bestimmten Eingabemuster eine zugehörige Ausgabeeinheit zu aktivieren.

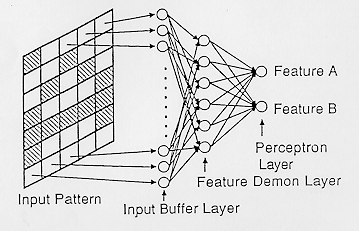
Bild 4: F.Rosenblatt (1958) PERCEPTRON-Netzwerk

Dazu gab es inhibitorische Verbindungen zwischen Ausgabe- und Assoziations-Schicht, die bewirkten, daß die erste aktive Ausgabe alle anderen möglichen Ausgabeeinheiten unterdrückte ("Winner-Take-All"-Prinzip). 1960 wurde von B.Widrow und M.Hoff ein vereinfachtes Perceptron, das "Adaline" (Adaptiv lineares Neuron, Bild 5) angegeben, dessen Lern-Algorithmus ("Delta-Regel") die Gewichte so einstellt, daß er den Fehler zwischen tatsächlicher und gewünschter Ausgabe minimiert.

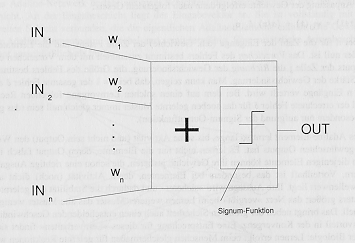
Bild 5: B.Widrow (1960) ADALINE-Netzwerk

Das Lernen konvergiert zwar schneller als beim Perceptron, jedoch nur in einem beschränkten Problembereich. Diesen sollte (Bild 6) das "Madaline" dadurch vergrößern, daß mehrere, parallel geschaltete Adalines mittels Majoritätsschaltung bewertet werden.

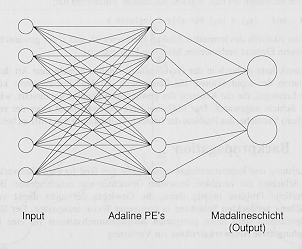
Bild 6: B.Widrow (1960) MADALINE-Netzwerk

Von K.Steinbuch wurde 1961 die "Lernmatrix" (Bild 7) vorgeschlagen, die mehrere Klassen unterscheiden kann. In der Lernphase erzeugt ein Satz von Eigenschaften mit einem Satz von dazugehörigen Bedeutungen an den Kreuzungen "bedingte Verknüpfungen" (durch Änderung von Widerstandswerten). In der Kannphase ist die Lernmatrix zweifach nutzbar: bei Eingabe von Eigenschaften wird die zugehörige Bedeutung (durch Extremwertbildung) ermittelt; Bei Eingabe der Bedeutung sind die entsprechenden Eigenschaften auszulesen.

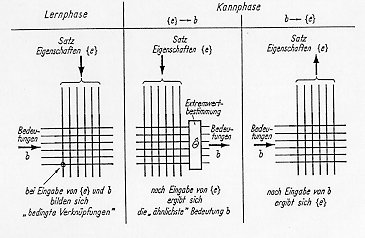
Bild 7: K.Steinbuch (1961) Lernmatrix

1.5. Die Kritik von Minsky und Papert

Mit der stürmischen Entwicklung von Nachrichtentechnik, Regelungstechnik und Systemtheorie trugen diese SNN-Experimente dazu bei, in der Kybernetik ein gemeinsames Ziel zu erkennen. In dieser romantischen Phase erschien 1969 das Buch "Perceptrons" von M.Minsky und S.Papert. Die Autoren zeigten, daß F.Rosenblatts "Konvergenz-Thoerem" für praktische Belange bedeutungslos ist : Perceptrons (und verwandte Schaltungen) können nur "linear-trennbare" Muster (vgl. Bild 8) lernen und klassifizieren, also "nichts interessantes" leisten. Falls mehrstufige Perceptrons "nicht-linear-trennbare" Probleme (z.B. XOR) lösen könnten , gäbe es aber infolge kombinatorischer Explosion keine Möglichkeit der korrekten Einstellung ihrer Gewichte.

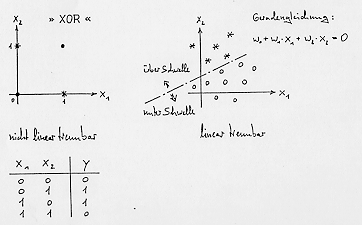
Bild 8: Lineare Trennbarkeit

1.6. Die weitere Entwicklung zum Durchbruch

Als Folge des negativen Urteils, von Minsky und Papert kam die Forschung auf dem Gebiet der SNN (durch Entzug der fiananziellen Förderung) praktisch zum Stillstand. Die Mehrheit versuchte KI durch Programmierung mit symbolverabeitenden Sprachen (z.B. LISP) zu erreichen. Zum Glück ließen sich einige Forscher davon aber nicht beeindrucken und arbeiteten weiter. Die nach und nach publizierten Ergebnisse gaben zu neuen Hoffnungen Anlaß. Einige Beispiele : T.Kohonen (1977) experimentierte mit Assoziativspeichern, die (im Gegensatz zur konventionellen Adressierung) ein gewünschtes Ausgabemuster (z.B. Passbild) über ein "Schlüssel"-Muster assoziieren. Dabei kann der Zugriffsschlüssel auch unvollständig (z.B. nur die Augenpartie enthaltend) und/oder verrauscht sein (Bild 9).

Bild 9: T.Kohonen (1977) Assoziativspeicher

J.Hopfield beschrieb 1982 einen Assoziativspeicher als Netzwerk mit internen Rückkopplungen (Bild 10). Die Prozessorelemente verfügen über "weiche" Schwellwertübergänge, die (statt 0 und 1) auch Zwischenwerte annehmen können.

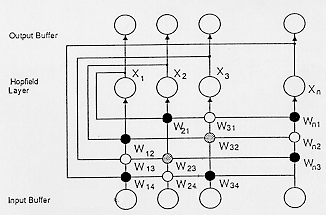
Bild 10: Hopfield-Netzwerk mit internen Rückkopplungen

Er deutete die Zuordnung von Eingangsschlüssel mit assoziiertem Ausgangswert als kollektives Einschwingen des Systems auf einen nahen Gleichgewichtszustand mit minimaler potentieller Energie. In der (n-dimensionalen) "Energielandschaft" entspricht jedes Tal einem gelernten (n-Tupel) Muster. Von G.Hinton und T.Sejnowski wurde diese "thermodynamische Modell" 1984 erweitert zur "Boltzmann-Maschine" mit der sie z.B. das kombinatorische "Problem des Handlungsreisenden" lösten. Um zu vermeiden, daß die Suche in einem lokalen Minimum hängen bleibt, benutzten sie als Schwellwertfunktion eine Sigmoid-Kurve (Bild 11) in der, der Parameter T als "Temperatur" gedeutet wird. Die Lösungssuche ("Simuliertes Ausglühen") beginnt bei hohen Temperaturen (starkes Schütteln der Energielandschaft; lokale Energiebarrieren können überwunden werden) endet bei T = 0.

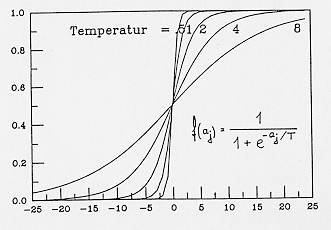
Bild 11: "Simul. Ausglühen" (simulated annealing)

Somit besteht eine gewisse Wahrscheinlichkeit zum Finden der optimalen Lösung. K.Fukushima stellte 1983 sein "Neokognitron" vor: Ein hierarchisch organisiertes Netz verknüpft die Ausgabe von trainierten "Merkmals-Detektoren" in übergeordneten Schichten und war dadurch fähig handgeschriebene Zeichen (Bild 12) trotz Deformation, Lage-Verschiebung und Rauschen richtig zu erkennen.

Bild 12: F. Fukushima (1983) NEOCOGNITRON Bsp. für richtig erkannte Handschriften

Einen weiteren Erfolg erzielten 1986 T.Sejnowski und C.Rosenberg mit "NETtalk". Sie brachten ihrem SNN bei, aus geschriebenem Englisch-Text, über eine Sprachausgabeeinheit, die richtigen Phonemketten zu generieren. Anfangs brabbelte das Netz wie ein Säugling. Nach jedem weiteren Trainingszyklus wurde die Aussprache deutlicher - bis nach etwa 50 Durchläufen nur noch wenige Fehler auftraten. Unbekannten Text las es dann völlig verständlich und machte die gleichen Fehler wie ein Englischanfänger. Das Netz hatte also die in den Beispielen versteckten Ausspracheregeln gelernt. Verglichen mit den kommerziellen Programm "DECtalk", in dem Mann-Jahre Entwicklungssaufwand steckten, welches die Sprachausgabe mittels Algorithmus realisierte, ist diese Leistung besonders beeindruckend. Das NETtalk-Projekt wurde in wenigen Wochen realisiert. 1986 veröffentlichten D.Rumelhart, J.McClelland und die "PDP-Group" (zu der auch G.Hinton und T.Sejnowski gehörten) ihre Forschungsberichte. Die Bücher wurden zum Bestseller und die von D.Rumelhart , G.Hinton und R.Williams entwickelte Lernstrategie "Backpropagation" zur populärsten für mehrlagige Netze. Das Entscheidende dabei sind die Prozessor-Elemente innerhalb (einer oder mehrerer) "verborgener" Schichten, deren Gewichte aber von der Backpropagation-Strategie trainierbar sind (was von Minsky und Papert als unmöglich angesehen wurde). Die Ergebnisse sind überzeugend, SNN ist der Durchbruch gelungen. Innerhalb der KI findet nun ein Paradigmenwechsel statt. Von den SNNs verspricht man sich den Ausweg aus der bestehenden Krise. Weitere Grundlagenforschung wird nun intensiv weltweit betrieben, entsprechende Fördermittel werden bereitgestellt und erste kommerzielle SNN-Anwendungen bewähren sich im Alltag (z.B. als [Plastik-] Sprengstoffdetektor zur Fluggepäcküberwachung).

1.7. Zwei Beispiele für das Lernen von Netzen

Das minimale "Backpropagation" - Netz zur Lösung des "XOR-Problems" besteht aus 3 Schichten, einer Eingangsschicht (zur Pufferung der Eingangswerte), einer verborgenen mit einem Prozessor-Element (PE) und einer Ausgangsschicht mit ebenfalls einem PE. Die PEs arbeiten hier wie das McCulloch-Pitts-Neuron (vgl. Bild 2). Die Zahlenwerte an den Verbindungen geben die Eingangsgewichte der PEs an. Bemerkenswert ist der zusätzliche Eingang #1 (mit 1=const). Über die zugeordneten Gewichte (vgl. W0 Bild 8) werden die Schwellen der PEs trainiert. Vor Trainingsbeginn werden alle Gewichte mit zufälligen Werten belegt (z.B. -0.2 .. +0.2). Für das Training ist die XOR-Wahrheitstabelle mit Eingangswerten und (gewünschtem) Ausgangswert verfügbar. Die Lernstrategie greift nun auf ein Eingabe-Wertepaar zu und propagiert die Information vorwärts unter Berücksichtigung der aktuellen Gewichte. Am Ausgang erscheint ein Ergebnis, das wahrscheinlich nicht mit dem gewünschten übereinstimmt. Der Fehler wird ermittelt und nun rückwärts (vom Ausgang zum Eingang) verfolgt, welche Gewichte welchen Einfluß auf das Ergebnis hatten. Ist ein Gewicht positiv oder negativ und sollte es auch sein, so wird es um einen kleinen Betrag vergrößert, andernfalls verkleinert. Im Laufe des Traíningszyklus werden viele Male Eingabe-Wertepaare angelegt, vorwärts berechnet, rückwärts korrigiert usw. bis sich alle Gewichte so eingestellt haben, daß das gewünschte Ergebnis erzielt wurde. Da hier alle möglichen Muster zum Training herangezogen wurden, ist diese Netz redundanzfrei und kann somit nur bedingt fehlertolerant sein.
Wir wollen noch einen "1-aus-n Decoder" (Bild 13) untersuchen, der keine direkten Verbindungen vom Ein- zum Ausgang hat. Wieviele PEs benötigen wir mindestens in der verborgenen Schicht ?

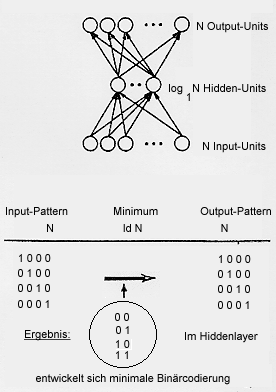
Bild 13: 1-aus-N Encoder-Netzwerk

Es ergibt sich, daß zur Codierung von n Zuständen ld n PEs benötigt werden. In diesen entwickelt sich eine minimale Binär-Codierung. Ein solches Netz kann zur Datenkompression genutzt werden. Das Ergebnis ist noch bemerkenswerter: In der verborgenen Schicht lassen sich innere Zustände ablesen, die zur Erklärung des Netzverhaltens herangezogen werden könnten. Beim Lernen ist i.A. auch Selbstorganisation (in ihrer einfachsten Form) zu beobachten. Falls Gewichte gegen Null konvergieren, hat diese Verbindung keinen Einfluß und kann entfernt werden. Beim Training können auch Probleme auftreten
(a) Infolge "linearer Abhängigkeit" (verschiedene Muster benutzen gemeinsame Gewichtspfade) kann es sein, daß bestimmte Muster nicht gelernt werden können.
(b) die Reihenfolge der Trainingsbeispiele kann für den Lernerfolg maßgeblich sein.
(c) Falls einige wenige Muster nicht gelernt werden kann man versuchen diese mehrfach in das Training aufzunehmen. Nach erfolgreichen Abschluß der Trainingsphase ist das "Wissen" ( möglicherweise nicht explizit bekannt ) im Netz verteilt in den Gewichten abgelegt worden. Das SNN beherrscht jetzt die Beispiele fehlerfrei und kann i.A. generalisieren (interpolieren und extrapolieren) und ist fehlertolerant. Je nach Bedarf könnte diese Netz dann entweder in Hardware (als Filter) oder als Softwaremodul realisiert und in Anwendungen eingebunden werden.

1.8. Stand der Forschungen

Die >>SNN<< befindet sich in stürmischer Entwicklung. Es gibt eine Vielzahl unterschiedlicher Ansätze. Diese zu beschreiben würde den Rahmen dieser Einführung sprengen. In Bild 14 sind wichtige Stichworte zur Orientierung zusammengestellt. Zur theoretischen Einarbeitung wird die angegebene Literatur empfohlen, über die weitere Quellen erschließbar sind.

Bild14: Abschließende Zusammenfassung