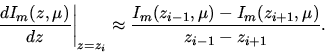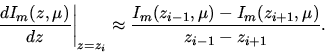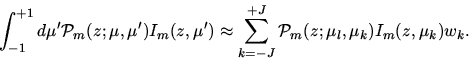Next: Danksagung
Up: Lösungstrategie in gometran
Previous: Separation der azimutalen Abhängigkeit
Nach der Entkopplung von azimutaler und zenitaler Winkelabhängigkeit
sind verschiedene Maßnahmen zu ergreifen, um die Diskretisierung
relevanter Größen in Hinblick der Implementierung des Modells als
numerischer Algorithmus zu ermöglichen.
Finite Differenzen: Ein wichtiger Schritt hinsichtlich
der Lösung der STG mittels finiter Differenzen ist die
Diskretisierung der Höhenvariablen z. Hierbei wird die Ableitung
des Strahlungsfeldes Im (siehe oben) für z=zi durch eine
,,endliche`` Differenz ersetzt:
Diskretisierung des Zenitwinkel: Ein weiterer
erforderlicher Schritt ist die Diskretisierung des Zenitwinkels.
Dieser Schritt ist insofern von Bedeutung, da er Konsequenzen für die
Raumwinkelintegration innerhalb der STG haben kann. In gometran wird die
GAUß-Quadratur benutzt. Sie verwendet die Nullstellen der LEGENDRE
Polynome (Press et al., 1989). Die Berechnung der Raumwinkelintegrale
erfolgt dann in folgender Form:
wk sind hierbei die Gewichte der Quadraturpunkte.
Symmetrische- und antisymmetrische Summe: Ein letzter
Schritt ist die Einführung sogenannter symmetrischer- und
antisymmetrischer Summen für die Strahlung. Sie stellen einen
weiteren Aspekt in der Entkopplung der nach oben und nach
untengehenden Strahlung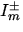 
dar. Sie werden abwechselnd auf
gerade und ungerade Höhenschichtindizes i angewendet. Die
symmetrische Summe J gilt für gerade Höhenschichtindizes, während
die antisymmetrische Summe H auf ungerade Höhenschichtindizes
angewendet wird:
Das gesamte Strahlungsfeld, also die Radianz für jede Höhe zi,
jeden Zenitwinkel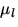 
und jede azimutal-harmonische Komponente
m wird schließlich durch die Lösung eines linearen
Gleichungssystems gefunden.
Marco Vountas
