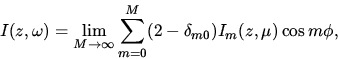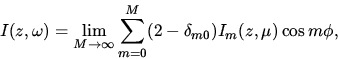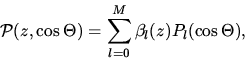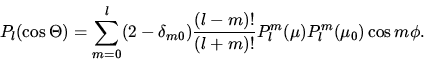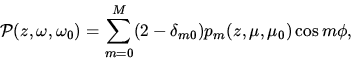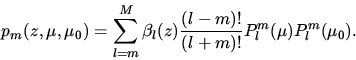Next: Diskretisierung
Up: Lösungstrategie in gometran
Previous: Lösungstrategie in gometran
Die STG kann in ein System von N Gleichungen überführt werden,
wenn eine Separation der azimutalen Abhängigkeit der Phasenfunktionen
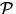 und Radianz I vorgenommen wird. Zunächst wird die
Entwicklung der Radianz rein formal als FOURIER Reihe mit den
Entwicklungskoeffizienten Im vorgenommen (mit
und Radianz I vorgenommen wird. Zunächst wird die
Entwicklung der Radianz rein formal als FOURIER Reihe mit den
Entwicklungskoeffizienten Im vorgenommen (mit
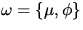 ):
):
| 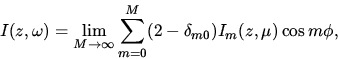 |
(1) |
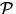 wird nun in eine LEGENDRE-Reihe bezüglich des Cosinus des
Streuwinkels
wird nun in eine LEGENDRE-Reihe bezüglich des Cosinus des
Streuwinkels 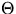 entwickelt:
entwickelt:
| 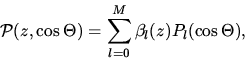 |
(2) |
mit den LEGENDRE-Polynomen 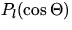 und
Entwicklungskoeffizienten
und
Entwicklungskoeffizienten 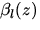 . Die eigentliche Separation der
azimutalen Abhängigkeit der Phasenfunktion ist erst möglich durch
die Einführung der assoziierten LEGENDRE-Polynome Plm. Die folgende
Beziehung (Vollständigkeitsrelation )
stellt den Zusammenhang zwischen den assoziierten und den herkömmlichen
LEGENDRE-Polynomen her:
. Die eigentliche Separation der
azimutalen Abhängigkeit der Phasenfunktion ist erst möglich durch
die Einführung der assoziierten LEGENDRE-Polynome Plm. Die folgende
Beziehung (Vollständigkeitsrelation )
stellt den Zusammenhang zwischen den assoziierten und den herkömmlichen
LEGENDRE-Polynomen her:
| 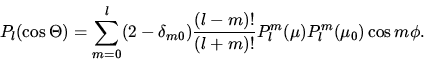 |
(3) |
Aus den Gleichungen 2 und 3 erhält man:
| 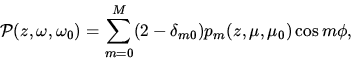 |
(4) |
mit
Setzt man nun Gleichung 1 sowie 4 in die STG
ein, zerfällt sie in M Gleichungen. Jede Einzelne ist mit Hilfe der
folgenden Annahmen lösbar und liefert Ergebnisse Im, die über die
oben genannte Summe (Gleichung 1) die Gesamtradianz
ergeben.
Marco Vountas