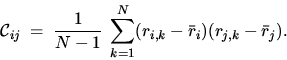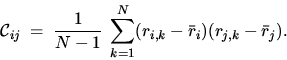Next: Anwendung auf Modell- und
Up: Die Hauptkomponenten der Auffüllung
Previous: Die Hauptkomponenten der Auffüllung
Die HOTELLING Methode hat sich in der
Orthogonalisierung von mehrdimensionalen Datensätzen etabliert. Mit
Hilfe der Transformation lassen sich lineare Abhängigkeiten aufdecken
und somit auch Aussagen darüber treffen, wie groß der
Informationsgehalt des Datensatzes ist. Die Methode hat ihren Ursprung
in der Stochastik und ist zum Beispiel in Papoulis (1984)
beschrieben.
Die statistischen Eigenschaften eines Datensatzes (Ensemble) sind
voneinander unabhängig, wenn nur die Hauptdiagonale (die Varianz) der
Kovarianzmatrix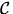 
von Null verschiedene Werte besitzt.
Die hier gestellte Aufgabe ist es, ein Ensemble mit bekannter
Kovarianz so zu transformieren, daß die (physikalischen)
Eigenschaften des Resultats erhalten bleiben, aber die Kovarianzen
verschwinden (das heißt, nur die Hauptdiagonale erhalten bleibt).
Die Kovarianzmatrix 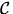von insgesamt N
Datenvektoren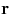 
ist definiert als:
In der hier konkret vorliegenden Aufgabe stellt ri,k das i-te
Element (spektraler Messwert) des k-ten Messpektrums von insgesamt
N Spektren dar.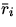 
ist der Mittelwert über alle i-ten
Elemente der insgesamt N Spektren. Eine andere (bequemere)
Schreibweise der Kovarianz(matrix) lautet wie folgt:
|  |
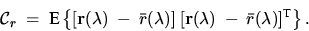(1) |
Hier ist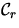 
die Kovarianz des Spektrenensembles
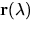. Die fettgedruckte Schreibweise symbolisiert, daß
es sich um einen Vektor mit N Elementen handelt, dessen Einträge
gerade den Spektren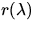 
entsprechen. Die Mittelwerte 
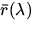werden über die Anzahl der Spektren gebildet. Der
Superskript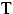 
symbolisiert die Transponierung.
In der selben Weise wie in Gleichung 10.1 läßt sich die
Kovarianz auch für einen orthonormalen Datensatz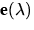 
formulieren, den es zu bestimmen gilt. Die Transformationsvorschrift
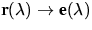basiert auf dem
einfachen linearen Zusammenhang:
|  |
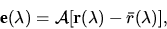(2) |
wobei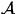 
der Transformationsmatrix entspricht. Nach
Einsetzen von Gleichung 10.2 in 10.1 und der
Forderung, daß der Zieldatensatz mittelwertfrei ist (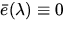
), ergibt sich mit 
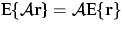und Gleichung 10.1:
|  |
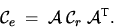(3) |
Da es Aufgabe ist, einen Datensatz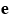 
zu entwickeln, der
orthonormal ist, wird seine Kovarianzmatrix 
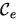eine
Diagonalmatrix sein. Unter der Bedingung, daß die
Transformationsmatrix 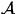orthogonal ist, läßt sich die
Gleichung 10.3 auch als
Eigenwertproblem in Matrixschreibweise auffassen. 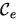ist dann eine Diagonalmatrix, die die Eigenwerte enthält. Die Zeilen
von 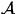enthalten die korrespondierenden Eigenvektoren.
Durch die Forderung nach Orthogonalität der (quadratischen) Matrix
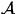ergibt sich weiterhin, daß die Zeilenvektoren von
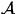ein orthonormales System darstellen.
Die Grundaufgabe für die Schaffung eines orthonormalen Datensatzes
mittels HOTELLING Transformation ist es also, die Eigenwerte 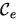und Eigenvektoren 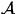der Kovarianzmatrix eines Ensemble von
Messpektren 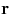zu bestimmen. Die Größe des damit geschaffenen
linear unabhängigen Datenraums ergibt sich schließlich aus dem
Signifikanzniveau, welches Eigenwerte unter einem vorgegebenen
Schwellwert zurückweist.
Das Verfahren basiert auf dem Ansatz, daß es sich bei den
Eingangsspektren um statistische Variablen handelt. Dies ist dieser
Arbeit nicht der Fall. Daher sind die physikalischen Eigenschaften der
durch die HOTELLING Transformation geschaffenen orthonormalen Basis im
nachhinein zu interpretieren.
In dieser Arbeit ist ausschließlich mit einer ,,nicht zentrierten``
Kovarianzmatrix (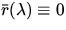
) für die Eingangsdaten
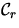gearbeitet worden. Dies hat zur Konsequenz, daß die
mittleren Eigenschaften des Ensemble nicht in die Bestimmung des
orthonormalen Systems eingehen können. Damit kann erreicht werden,
daß die signifikanten Eigenvektoren (solche unterhalb des
Signifikanzschwellwertes) das gesamte Ensemble besser approximieren
als Eigenvektoren, die für eine zentrierte Kovarianz bestimmt wurden.
Next: Anwendung auf Modell- und
Up: Die Hauptkomponenten der Auffüllung
Previous: Die Hauptkomponenten der Auffüllung
Marco Vountas
