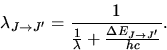Next: Zusammenfassung
Up: Mikroskopische Größen
Previous: Polarisierbarkeit und Dipolmoment
Die Theorie der RAYLEIGH und RAMAN Streuung ist in verschiedenen
Arbeiten, z.B.
(Long, 1977; Placzek & Teller, 1933; Placzek, 1934; Suschtschinskij, 1974; Weber, 1973) bereits
erschöpfend dargestellt worden. Es soll daher im folgenden nur eine
kurze Beschreibung der für Modellierung im Strahlungstransport
relevanten Größen geschehen.
Es besteht ein direkter Zusammenhang von RAYLEIGH- und RAMAN
Streuung: während bei der isotropen (bezüglich der
Polarisierbarkeit) RAYLEIGH Streuung, die im folgenden auch mit
CABANNES Streuung (Young, 1982) bezeichnet wird, die mittlere
Polarisierbarkeit  die Moleküleigenschaften des
Streuprozesses widergibt, ist es im Falle der RRS die Anisotropie
der Polarisierbarkeit
die Moleküleigenschaften des
Streuprozesses widergibt, ist es im Falle der RRS die Anisotropie
der Polarisierbarkeit  . Die anisotrope, spektral nicht
aufgelöste RAYLEIGH-Streustrahlung (Superskript: ,,ray``) ist die
Summe der Radianz der (isotropen) CABANNES-Streuung (Superskript:
,,cab``) und der der RRS-Linien (Superskript: ,,rrs``). Die von einem
Molekül RAYLEIGH-gestreute Radianz bei unpolarisierter Irradianz
I0 ist daher bestimmt durch:
. Die anisotrope, spektral nicht
aufgelöste RAYLEIGH-Streustrahlung (Superskript: ,,ray``) ist die
Summe der Radianz der (isotropen) CABANNES-Streuung (Superskript:
,,cab``) und der der RRS-Linien (Superskript: ,,rrs``). Die von einem
Molekül RAYLEIGH-gestreute Radianz bei unpolarisierter Irradianz
I0 ist daher bestimmt durch:
wobei  das Raumwinkelintervall für die einfallende Irradianz
ist,
das Raumwinkelintervall für die einfallende Irradianz
ist, 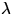 die Anregungswellenlänge und
die Anregungswellenlänge und 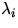 die insgesamt
L RRS Linienpositionen. N ist die Teilchenkonzentration, ds das
Wegintervall und
die insgesamt
L RRS Linienpositionen. N ist die Teilchenkonzentration, ds das
Wegintervall und 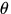 der Streuwinkel,
der Streuwinkel, 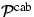 und
und 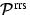 die
Phasenfunktionen, und
die
Phasenfunktionen, und 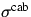 sowie
sowie 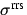 die Streuquerschnitte der
CABANNES Streuung und RRS. Die Abbildung 3.1 zeigt einen
fiktiven Versuchsaufbau, der den Zusammenhang der drei Streuprozeße
illustriert. Entlang der durch den Kegel dargestellten
Beobachtungrichtung wird ausschließlich Streulicht empfangen. Wenn
die resultierenden Photonen durch RAYLEIGH Streuung von ihrer
ursprünglichen Ausbreitungsrichtung abgebracht (
die Streuquerschnitte der
CABANNES Streuung und RRS. Die Abbildung 3.1 zeigt einen
fiktiven Versuchsaufbau, der den Zusammenhang der drei Streuprozeße
illustriert. Entlang der durch den Kegel dargestellten
Beobachtungrichtung wird ausschließlich Streulicht empfangen. Wenn
die resultierenden Photonen durch RAYLEIGH Streuung von ihrer
ursprünglichen Ausbreitungsrichtung abgebracht (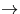 ,,Streuung im räumlichen Sinne``) wurden, so entstehen neben der
ursprünglichen Energie der Photonen weitere Energieniveaus
(
,,Streuung im räumlichen Sinne``) wurden, so entstehen neben der
ursprünglichen Energie der Photonen weitere Energieniveaus
(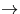 ,,Streuung bezüglich de Energie``). Das
charakteristische Muster, die sogenannten STOKES- und ANTI-STOKES
Linien, dieser Energieniveaus bildet sich um eine kräftige zentrale
Linie aus, welche auch CABANNES Linie genannt wird. Ist die spektrale
Auflösung des virtuellen Meßgerätes nicht groß genug, um die
STOKES- und ANTI-STOKES Linien über die ganze Bandbreite aufzulösen,
so ergibt sich die RAYLEIGH-gestreute Radianz.
,,Streuung bezüglich de Energie``). Das
charakteristische Muster, die sogenannten STOKES- und ANTI-STOKES
Linien, dieser Energieniveaus bildet sich um eine kräftige zentrale
Linie aus, welche auch CABANNES Linie genannt wird. Ist die spektrale
Auflösung des virtuellen Meßgerätes nicht groß genug, um die
STOKES- und ANTI-STOKES Linien über die ganze Bandbreite aufzulösen,
so ergibt sich die RAYLEIGH-gestreute Radianz.
Im folgenden werden die Größen 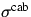 und
und 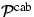 sowie
sowie 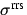 und
und
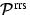 näher beschrieben und mit den Größen der ,,klassischen``
anisotropen RAYLEIGH Streuung
näher beschrieben und mit den Größen der ,,klassischen``
anisotropen RAYLEIGH Streuung 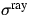 und
und 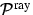 in Zusammenhang
gebracht.
in Zusammenhang
gebracht.
Größen der RAYLEIGH-Streuung
Die Beschreibung der relevanten Größen für die RAYLEIGH-Streuung
wird im folgenden auf der Basis von klassischen
(nicht-quantenmechanischen) Überlegungen durchgeführt, da auch die
praktische Umsetzung auf der Basis der klassischen Repräsentation
geschieht.
CABANNES Streuung (bezüglich der Polarisierbarkeit
isotrope RAYLEIGH Streuung): Für die spektral nicht
verschobene Streustrahlungskomponente ist bei isotroper
(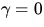 ) Polarisierbarkeit (der ursprüngliche Ansatz von
RAYLEIGH) die Richtungsabhängigkeit gegeben durch die auf
) Polarisierbarkeit (der ursprüngliche Ansatz von
RAYLEIGH) die Richtungsabhängigkeit gegeben durch die auf 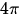 normierte Phasenfunktion
(Long, 1977):
normierte Phasenfunktion
(Long, 1977):
Die Wellenlängenabhängigkeit wird im (molekularen) Streuquerschnitt
zusammengefaßt. Die makroskopische Größe zur Beschreibung der
mittleren Polarisierbarkeit 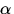 für Luft ist der
Brechungsindex n. Beide sind verknüpft über die sogenannte
LORENTZ-LORENZ'sche-Beziehung (in der Näherung für Gase) (Born, 1933):
für Luft ist der
Brechungsindex n. Beide sind verknüpft über die sogenannte
LORENTZ-LORENZ'sche-Beziehung (in der Näherung für Gase) (Born, 1933):
| 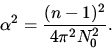 |
(1) |
wobei N0 die Loschmidtzahl ist. Im folgenden wird allerdings aus
Gründen der Übersichtlichkeit auf die Darstellung von 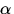 mittels n verzichtet, obwohl diese Schreibweise die in der
Literatur gängige ist und auch im Rahmen der Implementierung genutzt
wurde.
mittels n verzichtet, obwohl diese Schreibweise die in der
Literatur gängige ist und auch im Rahmen der Implementierung genutzt
wurde.
Anisotrope RAYLEIGH Streuung: Das von RAYLEIGH selbst
erweiterte klassische Modell der molekularen Streuung
berücksichtigte bereits ,,nicht-sphärische`` Streuteilchen.
Durch die Einbeziehung der nicht-isotropen Polarisierbarkeit hängt
die RAYLEIGH Streuung nun von 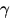 ab. Die für die Lichtstreuung
in Gasen notwendige räumliche Mittelung der nicht-isotropen
Polarisierbarkeit (
ab. Die für die Lichtstreuung
in Gasen notwendige räumliche Mittelung der nicht-isotropen
Polarisierbarkeit (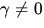 ) über alle räumlichen
Orientierungen der Streuzentren hatte weiterhin die implizite
Einbeziehung der Molekülrotation zur Folge. Die spektrale Auflösung
der RRS Linien erfolgt allerdings mit diesem Modell nicht.
Die spektral nicht-aufgelöste Radianz der RAYLEIGH Streuung ist für
) über alle räumlichen
Orientierungen der Streuzentren hatte weiterhin die implizite
Einbeziehung der Molekülrotation zur Folge. Die spektrale Auflösung
der RRS Linien erfolgt allerdings mit diesem Modell nicht.
Die spektral nicht-aufgelöste Radianz der RAYLEIGH Streuung ist für
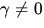 und unpolarisierte Irradianz unter anderem bestimmt
durch die auf
und unpolarisierte Irradianz unter anderem bestimmt
durch die auf 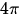 normierte
Phasenfunktion:
normierte
Phasenfunktion:
| 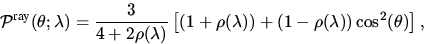 |
(2) |
wobei 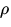 die Depolarisation, also die Abweichung von der
vollständigen Polarisation von RAYLEIGH-gestreutem Licht bei
90o Streuwinkel angibt (siehe auch Kapitel 7).
Sie ist abhängig von
die Depolarisation, also die Abweichung von der
vollständigen Polarisation von RAYLEIGH-gestreutem Licht bei
90o Streuwinkel angibt (siehe auch Kapitel 7).
Sie ist abhängig von 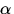 und
und 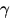 (siehe Anhang
B). Der Streuquerschnitt
(siehe Anhang
B). Der Streuquerschnitt
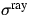 wird dann:
wird dann:
| 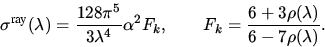 |
(3) |
Der Faktor Fk wird in der Literatur häufig als KING Faktor (nach
L.V. King (King, 1923)) bezeichnet (siehe
Anhang B). Im Rahmen dieser Arbeit kommt den
Gleichungen 2 und 3 besondere Bedeutung bei,
da sie in dieser Form auch im STM implementiert sind.
Allgemein besteht die gesamte Streustrahlung von räumlich frei
orientierbaren Systemen aus zwei Komponenten: einer im
räumlichen Sinne isotropen und einer anisotropen Komponente
(Long, 1977). Diese sind auf den symmetrischen- bzw.
antisymmetrischen Teil des Polarisierbarkeitstensors zurückzuführen.
Größen der RAMAN-Streuung
Die Intensität einer RRS Linie für einen Übergang zwischen den
Rotationsenergieniveaus EJ und EJ' hängt für eine Anzahl N
streuender Moleküle von der Summe der Besetzungswahrscheinlichkeiten
aller Anfangszustände der
Rotationsquantenzahl J, den
statistischen Gewichtsfaktoren gJ für die Anfangszustände
und der Irradianz I0 ab. Die in den gesamten
Raumwinkel Rotations - RAMAN- gestreute Radianz
(Schrötter & Klöckner, 1979) ist:
| 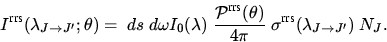 |
(4) |
Für das hier angenommene thermodynamische Gleichgewicht gehorcht
die Besetzungswahrscheinlichkeit der BOLTZMANN-Statistik, so daß die
Anzahl der Moleküle im Zustand J gegeben ist durch:
EJ ist die Energie des Anfangszustandes, k die BOLTZMANN
Konstante und T die Temperatur. Z ist die Zustandssumme und wie
folgt definiert:
Für den in dieser Arbeit angenommenen starren Rotator ist die
Rotationsenergie E als Funktion von J gegeben durch:
|
E(J) = h c B0 J ( J + 1 ),
| (5) |
wobei h das PLANCK'sche Wirkungsquantum, c die
Lichtgeschwindigkeit im Vakuum und B0 die Rotationskonstante des
betrachteten Moleküles im Vibrationsgrundzustand ist. Auf den
Streuquerschnitt 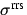 und die Phasenfunktion
und die Phasenfunktion 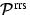 wird im
folgenden gesondert eingegangen.
wird im
folgenden gesondert eingegangen.
Richtungsabhängigkeit:
Die auf 4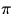 normierte Phasenfunktion
normierte Phasenfunktion 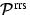 gibt die Richtungsabhängigkeit von RRS
(siehe auch Placzek (1934))
an. Für die Einstrahlung von unpolarisiertem Licht ergibt
sich:
gibt die Richtungsabhängigkeit von RRS
(siehe auch Placzek (1934))
an. Für die Einstrahlung von unpolarisiertem Licht ergibt
sich:
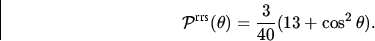 |
(6) |
Streuquerschnitt: 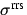 ist der Streuquerschnitt und
kann mit Hilfe der von Placzek begründeten
Polarisierbarkeitstheorie über die Invarianten des
Polarisierbarkeitstensors definiert werden. Für die Streuintensität
ist das Absolutquadrat der Matrixelemente des
Polarisierbarkeitstensors maßgebend. In der Abwesenheit von
äußeren Feldern sind für den Zustand J 2J+1 Zustände (
ist der Streuquerschnitt und
kann mit Hilfe der von Placzek begründeten
Polarisierbarkeitstheorie über die Invarianten des
Polarisierbarkeitstensors definiert werden. Für die Streuintensität
ist das Absolutquadrat der Matrixelemente des
Polarisierbarkeitstensors maßgebend. In der Abwesenheit von
äußeren Feldern sind für den Zustand J 2J+1 Zustände (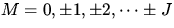 ) entartet. Daher muß die Summe der
Matrixelemente über alle möglichen Zustände der Quantenzahlen M
und M' bestimmt und hiernach durch die Entartung des
Anfangszustandes (2J+1) dividiert werden. Der Streuquerschnitt ist
nach räumlicher Mittelung und Zerlegung der Streustrahlung in
sogenannte Spur- und Anisotropiestreuung schließlich
(Placzek & Teller, 1933):
) entartet. Daher muß die Summe der
Matrixelemente über alle möglichen Zustände der Quantenzahlen M
und M' bestimmt und hiernach durch die Entartung des
Anfangszustandes (2J+1) dividiert werden. Der Streuquerschnitt ist
nach räumlicher Mittelung und Zerlegung der Streustrahlung in
sogenannte Spur- und Anisotropiestreuung schließlich
(Placzek & Teller, 1933):
| 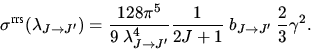 |
(7) |
Die Gleichung 7 beschreibt die spektrale
Abhängigkeit von RRS. Wie schon oben definiert wurde, handelt es
sich bei 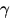 um die Anisotropie der Polarisierbarkeit.
Die Faktoren
um die Anisotropie der Polarisierbarkeit.
Die Faktoren 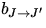 sind abhängig von der Auswahlregel und werden
weiter unten definiert.
Die Verschiebungswellenlänge
sind abhängig von der Auswahlregel und werden
weiter unten definiert.
Die Verschiebungswellenlänge 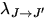 für den Übergang von J
nach J' korrespondiert über die Beziehung
für den Übergang von J
nach J' korrespondiert über die Beziehung 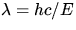 mit der
Energiedifferenz
mit der
Energiedifferenz 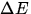 zwischen Anfangs- und Endzustand:
Die Größe der Energiedifferenz und damit der
Verschiebungswellenlänge ist bedingt durch die Auswahlregeln.
zwischen Anfangs- und Endzustand:
Die Größe der Energiedifferenz und damit der
Verschiebungswellenlänge ist bedingt durch die Auswahlregeln.
Auswahlregel: Die Auswahlregel für RRS ist 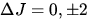 , wobei
, wobei 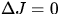 mit der (starken) spektral
unverschobenen CABANNES Linie korrespondiert und
mit der (starken) spektral
unverschobenen CABANNES Linie korrespondiert und 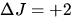 STOKES-Übergängen,
STOKES-Übergängen, 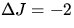 ANTI-STOKES-Übergängen entsprechen.
Mit Glg. 3.5 und der Auswahlregel ergibt sich
für STOKES-Übergänge
sowie für ANTI-STOKES-Übergänge
Weitere vom Rotationsübergang abhängige Größen sind die Faktoren
b
ANTI-STOKES-Übergängen entsprechen.
Mit Glg. 3.5 und der Auswahlregel ergibt sich
für STOKES-Übergänge
sowie für ANTI-STOKES-Übergänge
Weitere vom Rotationsübergang abhängige Größen sind die Faktoren
b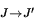 . Sie entsprechen der Rotationsabhängigkeit der
Betragsquadrate der mittleren Matrixelemente des
Polarisierbarkeitstensors und werden häufig auch als
PLACZEK-TELLER-Koeffizienten bezeichnet. Die Herleitung dieser
Faktoren für lineare (aber auch symmetrische Kreisel) Moleküle ist z.B.
Placzek & Teller (1933) zu entnehmen und sei hier nur erwähnt:
. Sie entsprechen der Rotationsabhängigkeit der
Betragsquadrate der mittleren Matrixelemente des
Polarisierbarkeitstensors und werden häufig auch als
PLACZEK-TELLER-Koeffizienten bezeichnet. Die Herleitung dieser
Faktoren für lineare (aber auch symmetrische Kreisel) Moleküle ist z.B.
Placzek & Teller (1933) zu entnehmen und sei hier nur erwähnt:
Abbildung 3.2 zeigt exemplarisch RRS Spektren für
O2 und N2, wobei die CABANNES Linie nicht dargestellt wurde.
Für beide Gase wurden jeweils zwei Wellenlängenbereiche ausgewählt.
Hierbei zeigt sich deutlich, daß der Einfluß von RRS zu kürzeren
Wellenlängen hin wächst. Der für N2 charakteristische
Intensitätswechsel benachbarter Linien geht auf die statistischen
Gewichte gJ zurück. gJ berücksichtigt, daß für die
Gesamtwellenfunktion aus Symmetriegründen nur bestimmte Werte des
Molekül-Kernspins erlaubt sind. Bei O2
fehlen für gerade J aus diesem Grund die Linien völlig. Die den
Berechnungen zugrundliegenden Daten sind im Anhang B
in Tabelle B.1 zusammengefaßt.
Next: Zusammenfassung
Up: Mikroskopische Größen
Previous: Polarisierbarkeit und Dipolmoment
Marco Vountas
![]() die Moleküleigenschaften des
Streuprozesses widergibt, ist es im Falle der RRS die Anisotropie
der Polarisierbarkeit
die Moleküleigenschaften des
Streuprozesses widergibt, ist es im Falle der RRS die Anisotropie
der Polarisierbarkeit ![]() . Die anisotrope, spektral nicht
aufgelöste RAYLEIGH-Streustrahlung (Superskript: ,,ray``) ist die
Summe der Radianz der (isotropen) CABANNES-Streuung (Superskript:
,,cab``) und der der RRS-Linien (Superskript: ,,rrs``). Die von einem
Molekül RAYLEIGH-gestreute Radianz bei unpolarisierter Irradianz
I0 ist daher bestimmt durch:
. Die anisotrope, spektral nicht
aufgelöste RAYLEIGH-Streustrahlung (Superskript: ,,ray``) ist die
Summe der Radianz der (isotropen) CABANNES-Streuung (Superskript:
,,cab``) und der der RRS-Linien (Superskript: ,,rrs``). Die von einem
Molekül RAYLEIGH-gestreute Radianz bei unpolarisierter Irradianz
I0 ist daher bestimmt durch:
![]() und
und ![]() sowie
sowie ![]() und
und
![]() näher beschrieben und mit den Größen der ,,klassischen``
anisotropen RAYLEIGH Streuung
näher beschrieben und mit den Größen der ,,klassischen``
anisotropen RAYLEIGH Streuung ![]() und
und ![]() in Zusammenhang
gebracht.
in Zusammenhang
gebracht.
![]() ) Polarisierbarkeit (der ursprüngliche Ansatz von
RAYLEIGH) die Richtungsabhängigkeit gegeben durch die auf
) Polarisierbarkeit (der ursprüngliche Ansatz von
RAYLEIGH) die Richtungsabhängigkeit gegeben durch die auf ![]() normierte Phasenfunktion
(Long, 1977):
normierte Phasenfunktion
(Long, 1977):