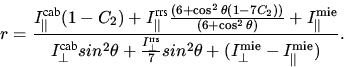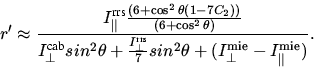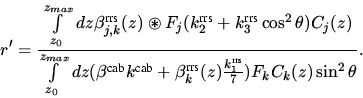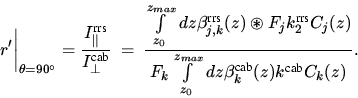Next: Modellierung von RING Referenz
Up: Messung von RING Referenz
Previous: Messung von RING Referenz
Die Standardformulierung des Ansatzes
Die Grundlage des Messansatzes nach Solomon et al. ist die
Annahme eines Polarisationsverhältnisses, das additiv aus einem
polarisierten und unpolarisierten Anteil besteht. Der polarisierte
Teil wird auf RAYLEIGH Streuung, der unpolarisierte auf RRS
zurückgeführt. Besonders in Hinblick auf die Diskussion in
Kapitel 4 ist dieser Ansatz in verschiedener Hinsicht
ungenau: (a) Die RAYLEIGH- gestreute Intensität beinhaltet bereits
die Rotations RAMAN- gestreute Intensität. Eine additive
Verknüpfung der elastischen Komponente der RAYLEIGH Streuung und
RRS wäre somit korrekt. (b) RRS ist nicht vollständig
unpolarisiert. (c) Neben der Vernachlässigung von MIE Streuung
basiert der Ansatz auf der Entkopplung der Streuprozesse, also der
additiven Verknüpfung der Strahlung für RAYLEIGH, MIE- und RRS.
Dies ist nur möglich, wenn Einfachstreuung vorliegt, eine
Annahme die im sichtbaren Wellenlängenbereich kaum- bzw. gar nicht
gültig ist.
Die zu messende Zielgröße, das RING Referenz Spektrum, basiert nach
Solomon et al. auf der Annahme, daß sich das zu messende
Polarisationsverhältnis 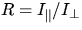 wie folgt ergibt:
wie folgt ergibt:
| 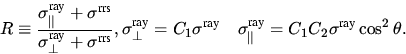 |
(1) |
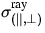 bezeichnet die mit den
Streuquerschnitten
bezeichnet die mit den
Streuquerschnitten 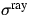 , also der von Polarisation und
Streuwinkel
, also der von Polarisation und
Streuwinkel 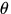 unabhängigen Größe, gewichteten
Phasenfunktionen der RAYLEIGH Streuung für die parallel
(,,
unabhängigen Größe, gewichteten
Phasenfunktionen der RAYLEIGH Streuung für die parallel
(,,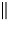 ``) bzw. vertikal (,,
``) bzw. vertikal (,,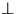 ``) polarisierte
Strahlungskomponente. C1 und C2 sind laut Solomon et al. 0.7629 bzw. 0.9324. In sie gehen aufgrund falscher
Annahmen bezüglich des Wellenbereichs zu groß gewählte
Depolarisationswerte der RAYLEIGH Phasenfunktion ein*. Der RRS Querschnitt
``) polarisierte
Strahlungskomponente. C1 und C2 sind laut Solomon et al. 0.7629 bzw. 0.9324. In sie gehen aufgrund falscher
Annahmen bezüglich des Wellenbereichs zu groß gewählte
Depolarisationswerte der RAYLEIGH Phasenfunktion ein*. Der RRS Querschnitt 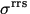 ist
wegen der Annahme der vollständigen Depolarisation nicht mit einem
Subskript versehen worden.
ist
wegen der Annahme der vollständigen Depolarisation nicht mit einem
Subskript versehen worden.
Die Gleichungen 1 sind in dieser Schreibweise nicht
korrekt, da bei der Bestimmung des Polarisationsverhältnisses
Intensitäten und nicht (gewichtete) Streuquerschnitte
ins Verhältnis gesetzt werden.
Das Verhältnis von Rotations-RAMAN- zu RAYLEIGH Streuquerschnitt
kompensiert spektrale Strukturen des RING Effekts bei
Spurengasauswertungen und wird daher häufig als RING Referenz Spektrum bezeichnet.
Solomon et al. berechnen es aus den
Gleichungen 1:
| 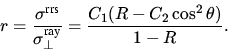 |
(2) |
Das so bestimmte RING Referenz Spektrum wird also für unterschiedliche
Streuwinkel entsprechend skaliert und ist daher für verschiedene
Sonnenstände bestimmbar. 3pt
Für  Streuwinkel (in diesem Fall der
Sonnenzenitwinkel) ergibt sich das Verhältnis von Rotations-RAMAN-
zu RAYLEIGH- Streuquerschnitt, zu:
Streuwinkel (in diesem Fall der
Sonnenzenitwinkel) ergibt sich das Verhältnis von Rotations-RAMAN-
zu RAYLEIGH- Streuquerschnitt, zu:
| 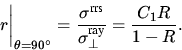 |
(3) |
Wobei 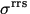 wegen der Annahme der vollständigen
Depolarisation nicht mit einem Subskript versehen wurde. Da r in
der DOAS Auswertung als skalierbares Referenzspektrum eingeht, ist ein
Faktor wie C1 nicht von Bedeutung.
wegen der Annahme der vollständigen
Depolarisation nicht mit einem Subskript versehen wurde. Da r in
der DOAS Auswertung als skalierbares Referenzspektrum eingeht, ist ein
Faktor wie C1 nicht von Bedeutung.
Ein entscheidender Vorteil des nach Gleichung 2
und 3 definierten RING Referenz Spektrums ist die
Einfachheit des Messprinzips, denn r hängt ausschließlich vom
Polarisationsverhältnis (und dem Streuwinkel) ab, was für die
Messung und spätere Datenverarbeitung eine bequeme
Grundlage darstellt und somit auch zur ,,Popularität`` dieser Methode
beigetragen hat.
Es stellt sich nun die Frage, welche Bedeutung das nach
Gleichung 2 gewonnene RING Referenz Spektrum hat, wenn der
atmosphärische Strahlungstransport einbezogen wird.
Die erweiterte Formulierung des Ansatzes
Die eigentliche Bedeutung des nach Gleichung 2
definierten RING Referenz Spektrums wird erst deutlich, wenn eine Analyse so
allgemein wie möglich erfolgt. Da keine analytische Lösung der STG
existiert, muß an dieser Stelle Einfachstreuung angenommen
werden (siehe Abschnitt 4). Die Bodenreflektion, die
praktisch auch Beitrag zur Einfachstreuung haben kann, wurde hierbei
nicht einbezogen.
Unter Einbeziehung des Strahlungstransports läßt sich
das am Boden im Zenit gemessene Polarisationsverhältnis, R,
mit der einfachgestreuten Intensität, I, wie folgt schreiben:
| 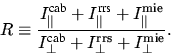 |
(4) |
Hierbei wurde die Strahlungskomponente der (rein) elastischen
Molekularstreuung mit 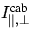 bezeichnet,
vergleiche mit Kapitel 4. Dieselbe Nomenklatur wurde
für die inelastischen Molekularstreuung, RRS,
,,
bezeichnet,
vergleiche mit Kapitel 4. Dieselbe Nomenklatur wurde
für die inelastischen Molekularstreuung, RRS,
,,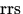 ``, und MIE- (Aerosolstreuung), ,,
``, und MIE- (Aerosolstreuung), ,,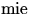 ``,
gewählt. Dabei bestimmen sich die jeweiligen Intensitätswerte wie
folgt:
``,
gewählt. Dabei bestimmen sich die jeweiligen Intensitätswerte wie
folgt:
| 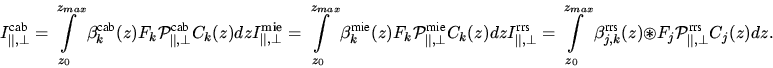 |
(5) |
Die Abkürzungen Ck und Cj sind für eine plan-parallele
Atmosphäre gegeben durch:
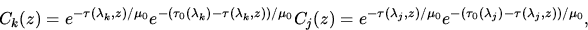
wobei die optische Dicke und totale optische Dicke mit 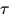 bzw.
bzw.
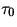 bezeichnet wurden sowie mit
bezeichnet wurden sowie mit 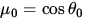 , dem Cosinus
des SZA.
Weiterhin sind folgende Abkürzungen eingeführt worden:
, dem Cosinus
des SZA.
Weiterhin sind folgende Abkürzungen eingeführt worden:
| 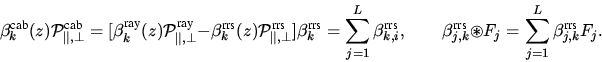 |
(6) |
Wie schon in Kapitel 4 ist Fk bzw. Fj der
extraterrestrische Fluß für die jeweilige Wellenlänge 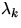 bzw.
bzw. 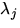 .
.  ,
, 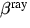 und
und 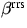 , bzw.
, bzw. 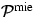 ,
,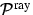 und
und 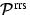 bezeichnen die Volumenstreukoeffizienten, bzw.
Phasenfunktionen für Aerosolstreuung sowie RAYLEIGH- und RRS für
die Höhe z.
bezeichnen die Volumenstreukoeffizienten, bzw.
Phasenfunktionen für Aerosolstreuung sowie RAYLEIGH- und RRS für
die Höhe z. 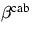 und
und 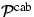 entsprechen den
Volumenstreukoeffizienten, bzw. Phasenfunktionen für elastische
(unverschobene) RAYLEIGH Streuung*. Im Sinne der
Übersichtlichkeit ist auf explizite Formulierung der
Winkelabhängigkeit für die Phasenfunktionen verzichtet worden.
entsprechen den
Volumenstreukoeffizienten, bzw. Phasenfunktionen für elastische
(unverschobene) RAYLEIGH Streuung*. Im Sinne der
Übersichtlichkeit ist auf explizite Formulierung der
Winkelabhängigkeit für die Phasenfunktionen verzichtet worden.
Die beiden Energieumverteilungsprozeße, also die
Verteilung der Energie, durch ,,Wellenlängenstreuung`` von allen
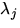 auf
auf 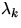 , sowie von
, sowie von 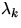 auf alle
auf alle
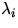 , wird durch
, wird durch 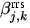 beziehungsweise durch
beziehungsweise durch 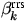 erfaßt.
erfaßt.
Setzt man nun Gleichung 4 in Gleichung 2
ein und führt weiterhin die Polarisationsverhältnisse für die
elastische Molekularstreuung sowie RRS (Placzek, 1934) ein:
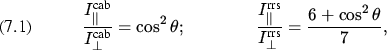
(7)
ergibt sich das gemessene RING Referenz Spektrum:
Für den Einsatz des RING Referenz Spektrums in der DOAS Auswertung wird ein
Polynom höherer Ordnung subtrahiert, um spektrale
Breitbandcharakteristika zu entfernen. Solche breitbandigen
Strukturen im RING Referenz Spektrum können nur durch ,,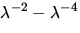 -Prozesse`` hervorgerufen werden, während durch die
Energieumverteilung, der Breitbandcharakteristik (
-Prozesse`` hervorgerufen werden, während durch die
Energieumverteilung, der Breitbandcharakteristik (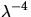 ) der
RRS die ,,hochfrequente`` Struktur (hochfrequent im Sinne der
spektralen Dynamik) der FRAUNHOFERlinien sowie Absorptionslinien aufgeprägt
wird. Da ein solches Meßspektrum üblicherweise Anwendung in der
DOAS Auswertung (siehe Abschnitt D) findet, ist die
Entfernung von breitbandige Strukturen mit Hilfe eines Polynoms
höherer Ordnung (Grad 2 bis 3) gewährleistet. Nach Abzug eines
Polynoms bezeichnet man r als differentielles RING Referenz Spektrum,
r'*:
) der
RRS die ,,hochfrequente`` Struktur (hochfrequent im Sinne der
spektralen Dynamik) der FRAUNHOFERlinien sowie Absorptionslinien aufgeprägt
wird. Da ein solches Meßspektrum üblicherweise Anwendung in der
DOAS Auswertung (siehe Abschnitt D) findet, ist die
Entfernung von breitbandige Strukturen mit Hilfe eines Polynoms
höherer Ordnung (Grad 2 bis 3) gewährleistet. Nach Abzug eines
Polynoms bezeichnet man r als differentielles RING Referenz Spektrum,
r'*:
| 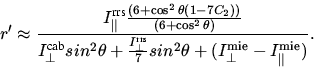 |
(8) |
Zu beachten ist bei der Interpretation eines nach
Gleichung 8 definierten differentiellen RING
Spektrums, daß neben der unmittelbaren Streuwinkelabhängigkeit,
bestimmt durch die Polarisationsverhältnisse- und Phasenfunktionen
(s.u.), noch die Abhängigkeit der optischen Dicke vom SZA
hinzukommt.
Aufgrund der Vielzahl atmosphärisch bedeutender Aerosole und ihrer
zum Teil stark unterschiedlichen optischen Eigenschaften ist es in
praxi nur schwer möglich, für den allgemeinen Fall das
Polarisationsverhältnis anzugeben. Allerdings liegt die
Depolarisation für ein polydisperses Aerosolgemisch fast immer
deutlich höher als für Molekularstreuung (für weitere Details
bezüglich der Polarisation des Tageshimmels sei auf Coulson (1988)
verwiesen). Weiterhin wird im kurzwelligen- sichtbaren sowie im
UV Wellenbereich Aerosoldepolarisation durch Mehrfachstreuung
maskiert. In Fällen starker urbaner Aerosolbelastung (z.B. Smog,
aber auch Bewölkung) muß sogar eine starke Zunahme der
(zusätzlich depolarisierenden) Mehrfachstreuung erwartet werden.
Damit darf für den hier dargestellten simplifizierten Ansatz
angenommen werden, daß die Differenz 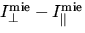 verschwindet. Für die Analyse realer
gemessener RING Referenz Spektren muß aber beachtet werden, daß bei moderater
Aerosolbelastung die Annahme der kompletten Depolarisation der
Aerosolstreuung nicht gegeben sein muß (Coulson, 1988)!
verschwindet. Für die Analyse realer
gemessener RING Referenz Spektren muß aber beachtet werden, daß bei moderater
Aerosolbelastung die Annahme der kompletten Depolarisation der
Aerosolstreuung nicht gegeben sein muß (Coulson, 1988)!
Die physikalische Bedeutung des RING Referenz Spektrums nach 8 wird
deutlich, wenn die Komponenten der Gleichung 8
mit 5 in eine ausführlichere Form gebracht werden. Neben
den spektralen Abhängigkeiten ist auch die Streuwinkelabhängigkeit
Gegenstand des Interesses. Daher sind für die Strahlungsterme
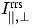 und
und 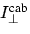 im folgenden die
Abhängigkeiten aufgeschlüsselt worden.
im folgenden die
Abhängigkeiten aufgeschlüsselt worden.
Es ergibt sich nun für das RING Referenz Spektrum bei Annahme der
vollständigen Depolarisation von Aerosolstreuung und Formulierung der
Phasenfunktionen (Kattawar et al., 1981) für die Strahlungsterme
| 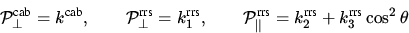 |
(9) |
folgender Zusammenhang:
| 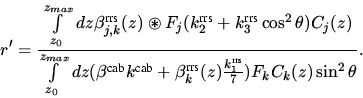 |
(10) |
Vernachlässigt man weiterhin aufgrund seiner Größe den RRS Term im
Nenner und gibt einen SZA von 90o vor, ist
das differentielle RING Referenz Spektrum demnach:
| 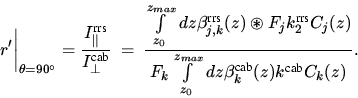 |
(11) |
Diskussion
Grundsätzlich trägt das nach Gleichung 10
und 11 definierte RING Referenz Spektrum beiden
,,Auffüllungsarten`` Rechnung: Auffüllung der FRAUNHOFERlinien sowie
Auffüllung der molekularen Absorptionslinien.
- 1.
- Die Auffüllung der FRAUNHOFERlinien erfolgt gemäß des Quotienten des
extraterrestrischen Flusses (Irradianz) für alle
Anregungswellenlängen
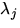 ,
, 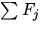 und dem Fluß für die untersuchte Wellenlänge
und dem Fluß für die untersuchte Wellenlänge 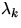 ,
,
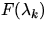 .
.
- 2.
- Die Auffüllung der Gasabsorptionslinien ist über
das integrale Verhältnis der Funktionen
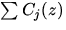 und Ck(z) bestimmt.
und Ck(z) bestimmt.
Weiterhin gewährleistet das so definierte RING Referenz Spektrum entsprechend
kleine Werte für den Fall geringer Dynamik des Sonnenspektrums
(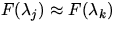 , sowie schwacher
Gasabsorption (
, sowie schwacher
Gasabsorption (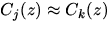 ). Gleichung 11 bestätigt die Annahme, daß im Falle
der Einfachstreuung bei 90o das durch R/(1-R) definierte
RING Referenz Spektrum dem Verhältnis RRS- zu elastisch- gestreuter Intensität
entspricht. Solomon et al. unterscheiden nicht zwischen
elastisch- gestreuter- und (klassisch) RAYLEIGH- gestreuter
Strahlung. Das von ihnen angegebene Verhältnis entspricht dem der
RRS- zu RAYLEIGH- gestreuten Intensität. Nach
Solomon et al.'s Ansatz ergibt sich das gemessene RING
Spektrum s entsprechend Gleichung* 3.
Zwischen der Definition für s gemäß Gleichung 3
und der für 90o SZA hier beschriebenen
(Gleichung 11), unter der Annahme, daß
). Gleichung 11 bestätigt die Annahme, daß im Falle
der Einfachstreuung bei 90o das durch R/(1-R) definierte
RING Referenz Spektrum dem Verhältnis RRS- zu elastisch- gestreuter Intensität
entspricht. Solomon et al. unterscheiden nicht zwischen
elastisch- gestreuter- und (klassisch) RAYLEIGH- gestreuter
Strahlung. Das von ihnen angegebene Verhältnis entspricht dem der
RRS- zu RAYLEIGH- gestreuten Intensität. Nach
Solomon et al.'s Ansatz ergibt sich das gemessene RING
Spektrum s entsprechend Gleichung* 3.
Zwischen der Definition für s gemäß Gleichung 3
und der für 90o SZA hier beschriebenen
(Gleichung 11), unter der Annahme, daß
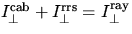 ,ergibt sich eine Beziehung zwischen r' und s von r'=s/(1-s).
Ist s also klein gegenüber 1, wird die Gleichung sich zu
,ergibt sich eine Beziehung zwischen r' und s von r'=s/(1-s).
Ist s also klein gegenüber 1, wird die Gleichung sich zu 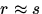 reduzieren. Dies gilt allerdings nicht im Bereich tieferer
FRAUNHOFERlinien, in denen die Rotations-RAMAN- gestreute Intensität große
Werte annehmen kann. Damit ergibt sich eine stärkere Auffüllung (der
molekularen Absorptionslinien sowie FRAUNHOFERlinien) als man sie gemäß
Formulierung nach Solomon et al. erwarten wird.
reduzieren. Dies gilt allerdings nicht im Bereich tieferer
FRAUNHOFERlinien, in denen die Rotations-RAMAN- gestreute Intensität große
Werte annehmen kann. Damit ergibt sich eine stärkere Auffüllung (der
molekularen Absorptionslinien sowie FRAUNHOFERlinien) als man sie gemäß
Formulierung nach Solomon et al. erwarten wird.
Im direkten Vergleich von r' und s bleiben allerdings
grundsätzliche Unsicherheitsfaktoren, die stark von der
atmosphärischen Situation während der Messung abhängen und somit
schwer vorhersagbar sind:
- 1.
- Mit Gleichung 7 läßt sich eine theoretische
Maximaldepolarisation des durch Rotations- RAMAN gestreuten Lichts
von 86% berechnen. Fraglich ist, wie sich die Forderung nach
vollständiger Depolarisation auf das gemessene RING Referenz Spektrum
auswirkt.
- 2.
- Welche Auswirkungen auf das gemessene RING Referenz Spektrum durch
Aerosolstreuung zu erwarten sind, bleibt unklar. Unter
Normalbedingungen ist sie nicht zu vernachlässigen.
- 3.
- Die depolarisierende Wirkung der Mehrfachstreuung wirkt sich auf
das RING Referenz Spektrum aus. Allerdings sind die Unsicherheiten dieser
Einflußnahme relativ groß: (i) Welchen Einfluß hat die durch RRS
mehrfachgestreute Strahlung? (ii) Wie wirkt sich die Aerosolstreuung im
Zusammenhang mit Mehrfachstreuung aus (
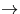 Wolken)?
Wolken)?
Es ist erwähnenswert, daß Richter für die
Bestimmung von s bei seinen Messungen den sinnvollen
Gültigkeitsbereich der Messungen von RING Referenz Spektren auf 50-90o SZA beschränkt:
- 1.
- da die Polarisation für SZA < 50o klein ist und damit
der Störabstand (SN) zu klein ist;
- 2.
- Da für große SZA > 90o die Integrationszeit
entsprechend groß gewählt werden muß, unterscheiden sich die
Lichtwege für die Messungen der unterschiedlichen
Polarisationsebenen. Damit können atmosphärische Absorptionen in
R erscheinen.
Weiterhin sind aufgrund des kleinen SN Zenitmessungen unterhalb von
320 nm nicht zuverlässig.
Zusammenfassung
Grundsätzlich bleibt zu bemerken, daß trotz zum Teil stark
vereinfachender Annahmen das nach Solomon et al. definierte
RING Referenz Spektrum ein Maß für die Größe des molekular-inelastisch zu
molekular-elastisch gestreuten Lichtes darstellt, obwohl, die Referenz
nicht, wie von Solomon et al. behauptet, die gesamte
RAYLEIGH-gestreute Intensität, sondern nach oben durchgeführten
Überlegungen nur die (unverschobene) Zentralkomponente der RAYLEIGH
Streuung ist. Für Vergleiche eines solchen RING Referenz Spektrums mit anderen
ist ein solcher Unterschied zu berücksichtigen.
Unabhängig von der Interpretation des RING Referenz Spektrums ist die
Unsicherheit, wie das gemessene RING Referenz Spektrum sich durch
Mehrfachstreuung verändert, da zum einen mehrfachgestreute
Strahlung normalerweise recht stark depolarisiert ist, zum anderen
auch RRS an der Mehrfachstreuung teilhat. Ein weiterer, entsprechend
großen Unsicherheitsfaktor stellt die Aerosolstreuung dar.
Im Abschnitt 9 werden verschiedene Meßspektren zwecks
Validation von Modelldaten benutzt. Eines davon ist das im September
1994 durch das GOME-FM (GOME Flight Model , das GOME
Flugmodell) gemessene RING Referenz Spektrum, welches gemäß der oben beschriebenen
Methode in Delft bei TPD während der GOME Kalibrationsphase bestimmt
wurde. Die genaue technische Spezifikation und Datenanalyse ist im
technischen Bericht von Richter et al. (1994) zu finden. Der Bestimmung
der RING Referenz Spektren für das bodengestützte Spektrometer in Bremen basiert
auf denselben Annahmen, wobei laut Richter et al. der
SN für die GOME-Messungen aufgrund weniger Messungen pro SZA
ungünstiger war.
Next: Modellierung von RING Referenz
Up: Messung von RING Referenz
Previous: Messung von RING Referenz
Marco Vountas
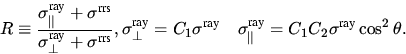
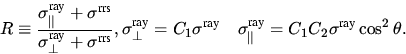
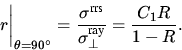
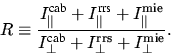
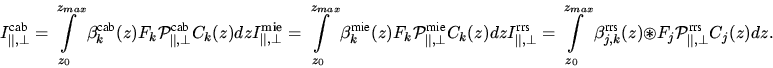
![]()
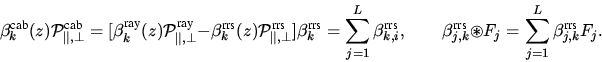
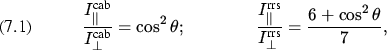 (7)
(7)