Next: Vergleich mit GOME Daten
Up: Validierung des Modells
Previous: Validierung des Modells
Wie bereits in Abschnitt 2.2 erörtert, stehen im Bereich
der Modellierung des RING Effektes außerordentlich wenig Modelle zur
Verfügung, die ausreichend dokumentiert und validiert wurden. Für
einen Vergleich mit einem anderen Modell kommt in erster Linie das
Modell einer Gruppe des GSFC (Goddard Space Flight Center ) der
NASA (National Aeronautics and Space Administration ) in Frage,
da das Modell ausführlich beschrieben wurde sowie konkrete Daten von
den Autoren (Joiner et al., 1995) erhältlich sind. Der Vergleich mit
einem anderen validierten Modell (Kattawar et al., 1981) scheiterte an der
unzureichenden Beschreibung und Verfügbarkeit der Daten, die in
einen solchen Vergleich eingehen (Burrows et al., 1996).
Das Modell der Gruppe des GSFC (im folgenden mit ,,GSFC Modell``
bezeichnet) basiert auf der Lösung der STG mittels der
,,successive order of
scattering``- Methode. Sie geht auf einen Vorschlag von Sekera
(1961) zurück und löst die STG auf iterativem Weg. Für den ersten
Iterationsschritt ergibt sich das primärgestreute Strahlungsfeld,
für den zweiten Schritt das sekundärgestreute usw. Die Methode
besitzt daher gegenüber anderen numerischen Methoden den Vorteil,
daß Ihre Resultate die physikalische Interpretation unterstützen.
Ein entscheidender Nachteil ist allerdings, daß die Konvergenz des
Verfahrens mit zunehmender Streuteilchendichte des Mediums abnimmt.
Der Vergleich der Modellresultate fokussiert sich auf die Auffüllung
der CaIIK Linie (vergleiche mit Anhang A).
Vergleich für simplifizierte Modellannahmen
Die Modellierung des RING Effektes im GSFC Modell erlaubt nicht die
Einbeziehung von Aerosolstreuung. Somit wurden die Werte für Phi in der CaIIK in Abhängigkeit des SZA zunächst nur für
Einfach- und Mehrfachstreuung (im folgenden wird der Begriff
Einfachstreuung mit SS und Mehrfachstreuung MS abgekürzt) ohne
Aerosolstreuung verglichen.
Die Ergebnisse beider Modelle sind im Bereich um 90o SZA
vergleichbar, da auch das GSFC Modell eine pseudo-sphärische
Approximation (siehe Abschnitt 6) der einfachgestreuten
Strahlung berücksichtigt.
Das GSFC Modell wurde ursprünglich zur Bestimmung von RING Spektren
für das SSBUV (siehe Abschnitt 2) entwickelt. Die
Modellergebnisse sind daher für Nadirbeobachtungen in
Satellitengeometrie bestimmt worden. Weiterhin wurde eine konservative
Atmosphäre angenommen. Bodenreflektion wurde zunächst nicht
einbezogen (A = 0). Die vom GSFC Modell genutzten Werte für die
Anisotropie der Polarisierbarkeit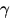 
bzw. die Depolarisation
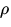(siehe Abschnitt 3 und Anhang B),
Druck und Temperatur, sowie das Irradianzspektrum des SSBUV und
konkreten Auffüllungswerte wurden freundlicherweise von J. Joiner zur
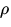Verfügung gestellt. Der angegebene Wert für lag für den
untersuchten Wellenlängenbereich deutlich zu hoch, wurde aber für diesen Vergleich trotzdem
angenommen. Da die gometran Berechnungen auf dem SSBUV Irradianzspektrum
als Eingangsgröße beruhen, ist die resultierende Auffüllung nur
für die spektrale Auflösung FWHM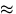 
1.1 nm (FWHM, engl.:
Full Width at Half Maximum , Halbwertsbreite) des SSBUV gültig
(nicht dargestellt ist der Einfluß der spektralen Auflösung auf die
Auffüllung. Für eine Untersuchung zu diesem Sachverhalt siehe
Bussemer (1993)).
Abbildung 9.1 zeigt die Modellergebnisse für SS
(links) und MS (rechts) im Vergleich. Beide Modelle
führen zu einem Anstieg der Auffüllung mit zunehmenden SZA. Dies
korrespondiert mit den Erfahrungen, die die meisten Experimentatoren
bei Bodenmessungen machten (Vergleiche mit Abschnitt 2.2).
Vergleich der SS Werte: Der Anstieg der Auffüllung mit
dem SZA ist maßgeblich bedingt durch die in Relation zu RAYLEIGH
Streuung isotrope Phasenfunktion. Einen
Überblick über die Phasenfunktionen gibt das Polardiagramm
9.2. Die HENYEY-GREENSTEIN
Phasenfunktion ist bereits dargestellt, obwohl Aerosolstreuung an
dieser Stelle noch nicht berücksichtigt wird.
Für SS bei Nadirbeobachtung entspricht der SZA gerade dem
Streuwinkel. In einem Bereich von 90o Streuwinkel steigen durch die
fast isotrope Phasenfunktion von RRS die
Wahrscheinlichkeit der inelastischen Streuung und somit die
Phi-Werte für SS.
Vergleich der MS Werte: Für MS bestimmt
zunächst die SS die SZA Abhängigkeit, aber zusätzlich ist ein
Anstieg der Auffüllung gegenüber den SS Auffüllungswerten zu
beobachten. Dies korrespondiert mit der Modellvorstellung, daß die
Anzahl der inelastischen Streuprozesse steigt. Die Auffüllung für
MS steigt zu großen SZA hin schneller als für SS. Auch dieses
Verhalten erklärt sich durch die stark-isotrope Phasenfunkion von
RRS, da mehrfachgestreute Strahlung (nicht nur aus der Richtung der
Sonne, sondern aus allen Richtungen) ähnlich stark gewichtet wird (im
Gegensatz zur RAYLEIGH Streuung).
Übereinstimmung der Resultate für beide Streumodi ist als gut zu
bezeichnen, wobei erwartungsgemäß die Resultate für SS deutlich
besser übereinstimmen als für MS. Da die Komplexität der Lösung
für MS wesentlich größer ist als für SS, sind zunehmende
Unterschiede zu erwarten gewesen. In beiden Fällen nehmen die
Differenzen zu großen Werten für den SZA ab. Dieses Verhalten ist
entsprechend stärker ausgeprägt für SS. Maximale Abweichungen
sind in beiden Fällen zwischen 60-80o zu beobachten. Der Grund,
warum in beiden Fällen gometran Werte durchweg größer sind, konnte
bisher nicht vollständig geklärt werden. Eine Schlüsselrolle für
die niedrigeren GSFC Werte im Fall der Mehrfachstreuung spielt aber
höchstwahrscheinlich die Einbeziehung einer begrenzten Anzahl an
Streuprozessen im GSFC Modell: hier wird zwar die Anzahl der
Streuprozesse in Hinblick auf Wellenlängenstreuung ebenso wie in gometran
auf eins beschränkt (also Streuung erster Ordnung, vergleiche auch
mit Kapitel 5), allerdings ist die gesamte Anzahl der
Streuprozesse, die ein Photon durchlaufen kann, höchstens acht. Im
Vergleich dazu ist die Anzahl der Streuprozesse in gometran nicht
beschränkt.
Vergleich bei Einbeziehung von Bodenreflektion und
Aerosolstreuung Ebenso wie gometran erlaubt das GSFC Modell die
Einbeziehung von LAMBERT'
scher Bodenreflektion. Von J. Joiner wurde Auffüllungswerte in
Abhängigkeit des SZA bei drei verschiedenen Bodenalbeden (A=0.08,
0.20, 0.95) bereitgestellt. Zunächst wurde keine Aerosolstreuung
einbezogen. Die Berechnungen von Joiner et al. (1995) mit Bodenreflektion
wurden ausschließlich für MS durchgeführt, daher wurde hier auf
eine Unterscheidung von MS und SS verzichtet.
Vergleich der gometran Phi-Werte mit und ohne Bodenreflektion
(ohne Aerosolstreuung): Der Vergleich der Abbildungen 9.1
(rechts) und 9.3 (links) zeigt, daß die Auffüllung mit
Berücksichtigung von Bodenreflektion für SZA kleiner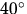 
unter
denen ohne Berücksichtigung von Bodenreflektion liegt, was zunächst
überraschend ist. Erwartungsgemäß gibt es für kleinere Albeden
(0.08 und 0.20) bei großen SZA kaum Unterschiede zu dem Ergebnis
ohne Bodenreflektion. Dieses Verhalten war zu erwarten, da für
große SZA der Einfluß der Bodenalbedo abnimmt.
Zwischen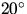 
und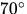 
SZA liegen die Werte mit
Berücksichtigung der Bodenalbedo über denen ohne Bodenreflektion.
Dies ist eine Konsequenz des LAMBERT'schen Reflektionsgesetzes,
welches in der Herleitung der STG angenommen wurde (siehe Abschnitt
4) und die Einstrahlung auf den Erdboden unter
großem Winkel schwächer gewichtet als kleine Winkel (Abhängigkeit:
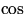(SZA)). Für kleine SZA ist die Auffüllung wiederum kleiner,
weil das Maximum der RAYLEIGH
Phasenfunktion in Rückwärtsrichtung (aber natürlich auch in
Vorwärtsrichtung) liegt und somit die ,,Menge`` des
elastisch-gestreuten Lichts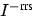 
entsprechend groß ist.
Vergleich der gometran-Phi Werte mit Bodenreflektion
untereinander (ohne Aerosolstreuung): Die Auffüllungwerte Phi der gometran Berechnungen (in Abbildung 9.3, links) sind für
mittlere Albeden (wie zum Beispiel A=0.2) für SZA bis etwa 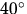am kleinsten. Die Bodenalbedo von 0.08 zeigt hier größte Werte, die
allerdings immer noch kleiner sind als für Berechnungen ohne
Bodenreflektion (Erklärung siehe unten). Dieses Verhalten kehrt sich
ab etwa 40o um: es ergeben sich zwar immer noch kleinste Werte
für eine Albedo von 0.2, aber das Maximum geht nun über zur
größten Albedo (A=0.95). Dieses Verhalten zeigt, daß die
zusätzliche Lichtmenge durch eine große Albedo nicht
notwendigerweise zu einer erhöhten Auffüllung führen muß. Hierfür
sind im wesentlichen zwei kontraproduktive Prozesse
verantwortlich:
- 1.
- Die stark-isotrope RRS Phasenfunktion kommt wie auch bei
großen SZA zum Tragen, wenn die LAMBERT'sche Abstrahlung unter
großen Winkeln geschieht. Zu Erklärung kann folgendes gedankliches
Modell hinzugezogen werden: Die LAMBERT'sche Reflektion führt zur
isotropen Abstrahlung. Die reflektierte Strahlung existiert damit
auch für sehr große Reflektionswinkel, unabhängig vom
Einfallswinkel. Gelangen solche Strahlen in die Sichtlinie des in
den Nadir blickenden Sensor, werden sie unter einem großen Winkel
gestreut. Dieser Prozeß gewinnt mit zunehmender Albedo an
Bedeutung für die Auffüllung.
- 2.
- Wie bereits in Abschnitt 5 dargestellt wird die
STG für die diffuse Strahlungskomponente bestimmt, die gesamte
Strahlung ist allerdings erst nach Addition der direkten
Strahlungskomponente vollständig bestimmt. Die direkte nach oben
gerichtete Strahlung war:
Dieser Term wird durch die Addition zur diffusen Strahlung in der
Auffüllung Phi nicht gekürzt werden können. Netto verbleibt
damit dieser Term daher im Nenner und führt somit zu einer
Verringerung der Auffüllung bei großer Bodenalbedo. Damit
erklären sich auch die allgemein niedrigeren Auffüllungswerte
gegenüber den Ergebnisse ohne Bodenreflektion für kleine
SZA.
Für kleine SZA ist der Einfluß beider Prozesse ähnlich stark, da
ansonsten kleinste Auffüllungswerte für große Albeden und umgekehrt
zu erwarten gewesen wären. Mit zunehmendem SZA steigt der Einfluß
des erstgenannten Effektes und damit ergeben sich größte Phi Werte für eine Albedo von 0.95.
Vergleich der Phi Werte mit Bodenreflektion der beiden
Modelle (ohne Aerosolstreuung): Die Auffüllungswerte von gometran (in
Abbildung 9.3, links) liegen wie schon für die Berechnungen
ohne Einbeziehung der Bodenalbedo (in Abbildung 9.1, rechts)
über denen des GSFC Modells.
Die Einbeziehung der Bodenreflektion
verstärkt allerdings die Unterschiede nochmals. Deutlich höhere
Werte von gometran für alle Albeden sind für mittlere SZA zu erkennen,
während die Differenz zwischen den Modellen für kleine SZA
(
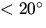) und große SZA (
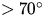) kleiner wird. Dieses Verhalten
war zu erwarten, da für kleine SZA der Einfluß der Auffüllung
abnimmt und für große SZA der Einfluß der Bodenalbedo abnimmt (und
damit ähnliche Ergebnisse wie in Abbildung 9.1 zu erwarten
sind). Beides führt zu einer Annäherung der Ergebnisse der beiden
Modelle. Für moderate Albeden, also Werte wie 0.08 und 0.20, sinkt
die Differenz für große SZA wieder (für die Albedo 0.95 sinkt die
Differenz ebenso, allerdings nicht signifikant). Dies war zu
erwarten, da die Bodenreflektion für große SZA an Bedeutung
verliert. Bei beiden Modellen sind die Phi Werte für eine Albedo
von 0.95 bei großen SZA am größten.
Für die große Albedo von 0.95 zeigen sich die Unterschiede beider
Modelle deutlicher als für die beiden kleineren Albeden. Die oben
erklärte Abstrahlung vom Erdboden unter großen Winkel ist bei gometran
stärker ausgeprägt als beim GSFC Modell.
Die Auffüllung in Abhängigkeit der Bodenreflektion ist bei beiden
Modellen bis 40o SZA ähnlich: Für den kleinsten Albedowert
(0.08) ergeben sich größte Auffüllungswerte; für eine Albedo von
0.20 sind die Werte am kleinsten; die Auffüllungswerte für eine
Albedo von 0.95 liegt zwischen den beiden erstgenannten Ergebnissen.
Für SZA größer 40o liegen die Auffüllungswerte von gometran für
eine Albedo von 0.95 am höchsten. Dies ist beim GSFC Modell erst ab
80o zu beobachten.
Die für gometran Auffüllungen beobachtete Abnahme der Auffüllung
verglichen mit dem Beispiel ohne Reflektion zeigt sich noch deutlicher
bei dem GSFC Modell. Hier liegen bis etwa 70o SZA alle
Auffüllungswerte unter denen ohne Einbeziehung von Bodenreflektion.
Vergleich der gometran-Phi Werte mit Bodenreflektion
untereinander (mit Aerosolstreuung): Die Auffüllungwerte Phider gometran Berechnungen (siehe Abbildung 9.3, rechts)
zeigen hier deutlich, daß die Aerosolstreuung den Effekt der
Abstrahlung unter großem Winkel unterdrückt. Der Erklärung hierfür
ist die HENYEY-GREENSTEIN Phasenfunktion (siehe Abbildung 9.2), die für
Streuwinkel um die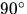 
kein Minimum wie die RAYLEIGH
Phasenfunktion hat und somit die Isotropie der RRS Phasenfunktion
nicht zum tragen kommt. Daher ergibt sich der dominante Einfluß der
direkt-reflektierten Strahlung und somit die kleinsten
Auffüllungswerte für die größte Albedo und umgekehrt. Für sehr
große SZA nähern sich die unterschiedlichen Ergebnisse an.
Vergleich der Phi Werte mit Bodenreflektion der beiden
Modelle (mit und ohne Aerosolstreuung): Die Abbildung 9.3
rechts oben zeigt, daß die Ergebnisse deutlich unter denen, die ohne
Aerosolstreuung gerechnet wurden, liegen. Dies wird mit oben
Erklärtem klar: der dominante Einfluß durch die direkt-reflektierte
Strahlung ergibt sich in erster Linie eine Schwächung durch die
Bodenreflektion. Die Abstrahlung unter großem Winkel ist relativ (zur
Aerosolstreuung) betrachtet zu klein, als daß sie signifikanten
(positiven) Beitrag zur Auffüllung liefern kann.
Allgemein zeigt sich, daß die Modellierung der Bodenreflektion in gometran
relativ deutliche Unterschiede in der Auffüllung
produziert. Die Einbeziehung von Aerosolstreuung führt zu
entsprechend deutlichen Unterschieden.
Nicht dargestellt sind Untersuchungen mit unterschiedlich großen
Aerosolkonzentrationen- und Typen. Erste Ergebnisse in dieser
Richtung zeigen eine große Variabilität der Auffüllung bezüglich
Aerosolkonzentration- und Typ.
Next: Vergleich mit GOME Daten
Up: Validierung des Modells
Previous: Validierung des Modells
Marco Vountas
